RASCHETA.NET
Общие сведения о построении эпюр внутренних усилий в балках.
Определить внутренние усилия в любом поперечном сечении однопролетных балок с разными граничными условиями (закреплениями) и построить эпюры этих поперечных усилий от при воздействии различных видов нагрузки (сосредоточенная, равномерно распределенная и т.д. ), мы можем с помощью простейших уравнений предмета - строительная механика. Перед тем как приступить к рассмотрению основных зависимостей и положений используемых при построении эпюр необходимо напомню Вам правила знаков, принятые при построении эпюр усилий: 1. Поперечная сила Q является положительной, если в левой стороне правой части балки её ориентация имеет направление сверху вниз, и на правой стороне левой части ориентация - сверху вниз. При этом на эпюре поперечных сил положительное значение ординаты откладывает по направлению вверх от оси и соответственно отрицательное – вниз. 2. Изгибающий момент M положителен, если на левой стороне правой части балки момент имеет направление по часовой стрелке, а на правой стороне левой части - против часовой стрелки. В этом случае при построении эпюр момента положительное значение ординаты откладывает по направлению вниз и соответственно отрицательное – вверх. 3. Продольная сила N является положительной, если она приводит к удлинению, а отрицательной, если приводит к сжатию. И на эпюре соответственно положительное значение откладывает вверх и отрицательное – вниз.

Рассмотрим основные зависимости между изгибающим моментом, поперечной силой и нагрузкой, которые в дальнейшем нам позволят определить правильность построения эпюр и упростят их построение.
Первую и основную зависимость можно представить в виде:
![]()
Тем самым, поперечная сила является функцией от производной в первой степени от изгибающего момента по абсциссе поперечного сечения балки.
Соответственно интенсивность нагрузки равна производной от поперечной силы.
![]()
Применяя эти зависимости, мы можем получить основные положения, которыми можно воспользоваться при построении эпюр:
1. Если поперечная сила на эпюре имеет значение равное нолю, то изгибающий момента имеет в этой точке максимальные или минимальные значения.
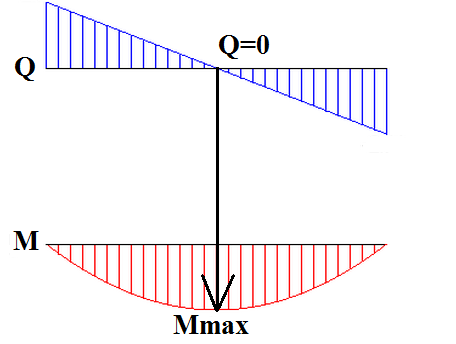
2. На участке с убыванием значения эпюры М значения поперечного усилий Q имеют отрицательные значения, а участки с увеличением значения эпюры M имеют положительные значения Q - поперечной силы.

3. Численное значение Q поперечной силы соответствует «тангенсу» угла образованного касательной к эпюре изгибающего момента М и продольной осью балки.

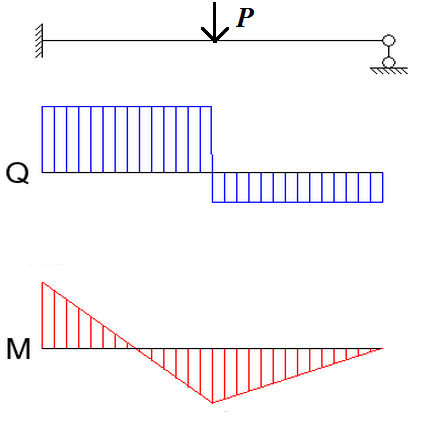
4. Если на балку действуют только сосредоточенные усилия то эпюра Q является горизонтальной линией ( или несколько горизонтальных линий), а эпюра М также имеет линейный характер и как правило наклонный.
5. В случае действия на балку распределенного усилия q эпюра Q поперечной силы является наклонной, при этом эпюра М будет представлена в виде квадратной параболой.

6. При действии на балку распределенной нагрузки изгиб эпюры изгибающего момента направлена в ту же сторону что и действующая нагрузка.

7. В сечении балки, в точке воздействия поперечной силы, образуется характерный перегиб эпюры М и сдвиг(скачок) в эпюре Q поперечной силы. Абсолютное значение данного сдвига равно значению приложенной поперечной силы.

8. Площадь эпюры поперечной силы на определенном участке соответствует изменению значению изгибающего момента по длине данного участка.

9. Площадь эпюры q распределенной нагрузки численно равно изменению поперечной силы по длине данного участка.

1. Ось, относительно которой откладывается эпюра, должна быть параллельна продольной оси балки.
2. Ординаты, численно равные значениям усилий необходимо откладывать от оси перпендикулярно.
3. Эпюры усилий штрихуются прямыми линиями перпендикулярными к принятой оси.
4. На характерных точках эпюры (перегибы, максимальные и минимальные значения) целесообразно проставлять значения усилий с указанием знака усилия.
Так же важно отметить, что при действии на балку нескольких нагрузок(усилий), то результирующая эпюра поперечных сил и изгибающих моментов складывается из эпюр усилий, полученных от каждой нагрузки в отдельности-принцип независимости(суперпозиций) действия сил. Данный принцип относиться и к расчетам по определению прогиба(изгиба) балки.